【小故事】
爱因斯坦曾写道:“在我一生中,还没有如此勤奋工作过,我已沉湎于数学的伟大,直到今天,我一直在领略,我一直在领略数学的微妙部分的纯正的高贵”。
【知识讲堂】

① 平行四边形相邻两边之和等于周长的一般;
② 平行四边形被对角线分成的四个小三角形中,相邻两个三角形的周长之差等于相邻两边之差

3.从中心对称的角度找全等
已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
(1)观察图形并找出一对全等三角形:△ ≌△ ,请加以证明;
(2)在(1)中你所找出的一对全等三角形,其中一个三角形可由另一个三角形经过怎样的变换得到?

6.平行四边形中点的问题解决
如图,在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54°,则∠B=( )
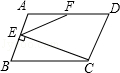
A.54° B.60° C.66° D.72°
【方法解读】
对角线是解决四边问题的常用线段,对角线本身的特性可以确定四边形的形状、大小,连对角线后,平行四边形就得到三角形,这样我们就能:
(1) 利用三角形的三边关系,判定平行四边形的构成情况;
(2) 借助三角形的面积,解决相关平行四边形的面积问题。
【答案】
1.A.2.B.3.(1)△DOE≌△BOF;△BOM≌△DON;△ABD≌△CDB.(2)绕点O旋转180°后得到或以点O为中心作对称变换得到.
4. 如图所示:
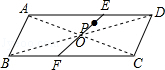
连接AC、BD相交于点O,过O、P作直线分别交AD、BC于E、F,
则一人分四边形ABFE,另一人分四边形CDEF.
5.D 6.D





