北京期末初中一次函数

    点击领取→期末必刷冲刺复题目：北京初一/二/三上学期期末试题及答案解析(持续更新中，建议收藏)

北京期末初中一次函数！学习的时候不仅要看到书面上，而且还要看到书背后。这就是说，对书本的某些原理、定律、公式，不仅应该记住它的结论，懂得它的道理，能够灵活地运用它，而且还应当设想一下人家是怎样想出来的。下面，小编为大家带来北京期末初中一次函数。

北京期末初中一次函数

1、一次函数的定义

一般地，形如（k，b是常数，且k≠0）的函数，叫做一次函数，其中x是自变量。当b=0时，一次函数y=kx，又叫做正比例函数。

⑴一次函数的解析式的形式是，要判断一个函数是否是一次函数，就是判断是否能化成以上形式．

⑵当b=0，k≠0时，y=kx仍是一次函数．

⑶当k=0，b≠0时，它不是一次函数．

⑷正比例函数是一次函数的特例，一次函数包括正比例函数．

2、正比例函数及性质

一般地，形如y=kx(k是常数，k≠0)的函数叫做正比例函数，其中k叫做比例系数.

注：

正比例函数一般形式 y=kx (k不为零)

① k不为零 ② x指数为1 ③ b取零

当k>0时，直线y=kx经过一、三象限，从左向右上升，即随x的增大y也增大；

当k<0时，直线y=kx经过二、四象限，从左向右下降，即随x增大y反而减小．

(1) 解析式：y=kx（k是常数，k≠0）

(2) 必过点：（0，0）、（1，k）

(3) 走向：k>0时，图像经过一、三象限；k<0时，图像经过

二、四象限

(4) 增减性：k>0，y随x的增大而增大；k<0，y随x增大而减小

(5) 倾斜度：|k|越大，越接近y轴；|k|越小，越接近x轴

点击了解>>>终于等到你！学而思8人班期末真题刷题班，针对性训练更快，赶快点击链接了解吧~&咨询课程请拨打：

3、一次函数及性质

一般地，形如y=kx＋b(k,b是常数，k≠0)，那么y叫做x的一次函数.当b=0时，y=kx＋b即y=kx，所以说正比例函数是一种特殊的一次函数.

注：一次函数一般形式 y=kx+b (k不为零)

① k不为零

②x指数为1

③ b取任意实数

一次函数y=kx+b的图象是经过（0，b）和（-b/k，0）两点的一条直线，我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到.（当b>0时，向上平移；当b<0时，向下平移）

（1）解析式：y=kx+b(k、b是常数，k≠0)

（2）必过点：（0，b）和（-b/k，0）

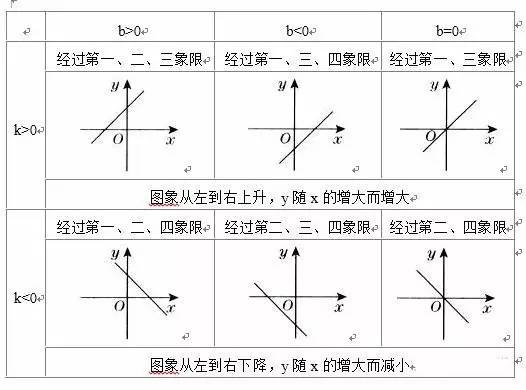
（3）走向：

k>0，图象经过先进、三象限；k<0，图象经过第二、四象限

b>0，图象经过先进、二象限；b<0，图象经过第三、四象限

直线经过先进、二、三象限

直线经过先进、三、四象限

直线经过先进、二、四象限

直线经过第二、三、四象限

（4）增减性： k>0，y随x的增大而增大；k<0，y随x增大而减小.

（5）倾斜度：|k|越大，图象越接近于y轴；|k|越小，图象越接近于x轴.

（6）图像的平移：

当b>0时，将直线y=kx的图象向上平移b个单位；

当b<0时，将直线y=kx的图象向下平移b个单位.

4、一次函数y=kx＋b的图象的画法.

根据几何知识：经过两点能画出一条直线，并且只能画出一条直线，即两点确定一条直线，所以画一次函数的图象时，只要先描出两点，再连成直线即可.一般情况下：是先选取它与两坐标轴的交点：（0，b），（-b/k，0） .即横坐标或纵坐标为0的点.

 

话仿佛是自己说的，文章仿佛是自己写的，只有消化了，才能在这个基础上创造出新的东西来，不然人云亦云，世界就没有发展了。想了解相关课程的同学，请拨打学而思爱智康免费咨询电话：！

北京期末初中一次函数就给大家分享到这里，另外学而思学科老师还给大家整理了一份《初一期末试题资料合集》。

  点击领取：《期末必刷冲刺复题目：北京初一/二/三上学期期末试题及答案解析(持续更新中，建议收藏)》

查缺补漏，助你备战期末！

部分资料截图如下：

点击链接领取完整版资料：https://jinshuju.net/f/Ggc9gd

同时也向您的孩子推荐终于等到你！学而思8人班期末真题刷题班，针对性训练更快，赶快点击链接了解吧~，点击链接：https://editor.izhikang.com/#/preview?&uid=b576b4e7a0615e6a57f19b4a7a388b2e&entrySource=40fa31849d511d84ad1c6f56c9bf4bcf&extendionSource=QT001 或者下方图片即可预约

相关推荐：

① 北京期末初中函数题

② 北京期末初中数学二次函数