高中数学导数构造函数题

2021-09-15 14:56:32 来源：佚名

免费领取新学期学习资料

单元测试卷丨学科知识同步丨期中期末卷等

高中数学导数构造函数题！同学们数学是所有理科生的基础，数学与理化生的学习也是相辅相成的。数学学好了，理化生自然也学的好。反之，数学学不好，理化生更是无从下手。同学们一定要做好准备。下面，小编为大家带来高中数学导数构造函数题。

导数概念的引入

1. 导数的物理意义：

瞬时速率。一般的，函数y=f(x)在x= 处的瞬时变化率是

2. 导数的几何意义：

曲线的切线，当点趋近于P时，直线 PT 与曲线相切。容易知道，割线的斜率是

当点趋近于 P 时，函数y=f(x)在x=处的导数就是切线PT的斜率k，即

3. 导函数：

当x变化时，便是x的一个函数，我们称它为f（x）的导函数. y=f（x）的导函数有时也记作。

导数的计算

基本初等函数的导数公式：

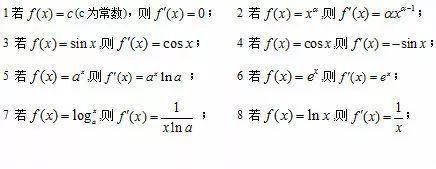
导数的运算法则：

复合函数求导：

y=f(u)和u=g(x)，则称y可以表示成为x的函数，即y=f(g(x))为一个复合函数。

以上是部分资料截图，点击下方链接领取完整版

转化与化归思想

转化与化归是中学数学最基本的数学思想之一，是一切数学思想方法的核心。数形结合的思想体现了数与形的转化；函数与方程的思想体现了函数、方程、不等式之间的相互转化；分类讨论思想体现了局部与整体的相互转化，所以以上三种思想也是转化与化归思想的具体呈现。

转化包括等价转化和非等价转化，等价转化要求在转化的过程中前因和后果是充分的也是必要的；不等价转化就只有一种情况，因此结论要注意检验、调整和补充。

转化的原则是将不熟悉和难解的问题转为熟知的、易解的和已经解决的问题，将抽象的问题转为具体的和直观的问题；将复杂的转为简单的问题；将一般的转为特殊的问题；将实际的问题转为数学的问题等等使问题易于解决。

常见的转化方法：

①直接转化法：把原问题直接转化为基本定理、基本公式或基本图形问题；

②换元法：运用“换元”把式子转化为有理式或使整式降幂等，把较复杂的函数、方程、不等式问题转化为易于解决的基本问题；

③数形结合法：研究原问题中数量关系（解析式）与空间形式（图形）关系，通过互相变换获得转化途径；

④等价转化法：把原问题转化为一个易于解决的等价命题，达到化归的目的；

⑤特殊化方法：把原问题的形式向特殊化形式转化，并证明特殊化后的问题，使结论适合原问题；

⑥构造法：“构造”一个合适的数学模型，把问题变为易于解决的问题；

⑦坐标法：以坐标系为工具，用计算方法解决几何问题也是转化方法的一个重要途径。

以上就是小编特意为大家整理的高中数学导数构造函数题的相关内容，同学们在学习的过程中如有疑问或者想要获取更多资料，请拨打学而思爱智康免费咨询电话：400-810-2680！

部分资料截图如下：

点击链接领取完整版资料：https://jinshuju.net/f/fzH4Lv