平面与圆柱面的截线考点

　　平面与圆柱面的截线考点！平面与圆柱面的截线是高中的学习重点，同学们学习这部分内容的时候，应该了解章节考点，科学学习。下面小编为大家分享平面与圆柱面的截线考点!希望对大家有所帮助！

 

 

平面与圆柱面的截线大汇总

 

　　平面与圆柱面的截线考点

 

1、平面与圆柱面的截线

探究讨论：如图3-5(课本第45页)，AB，CD是两个等圆的直径，AB//CD，AD、BC均与两圆相切.作公切线EF，切点分别为F₁和F₂ ，交BA，DC的延长线与E，F，交AD于G₁，交BC于G₂，设EF与BC，CD的交角分别为φ，θ.21cnjy.com

由切线长定理有

G₂F₁＝G₂B，G₂F₂＝G₂C，

∴G₂F₁＋G₂F₂＝G₂B＋G₂C＝BC＝AD

又∵G₁G₂＝G₁F₂＋F₂G₂

由切线长定理知

G₁F₂＝G₁D，F₂G₂＝G₂C，

∴G₁G₂＝G₁D＋G₂C

连接F₁O₁，F₂O₂，容易证明

△EF₁O₁≌△FF₂O₂

∴EO₁＝FO₂

又∵O₁A＝O₂C，

∴EA＝FC

于是可证得△FCG₂≌△EAG₁

∴G₁A＝G₂C

∴G₁G₂＝G₁D＋G₁A＝AD

在Rt△G₂EB中

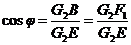
∴ G₂F₁=G₂Ecosj

又 ∵ j=90°-q

∴ G₂F₁=G₂Ecosj=G₂Esinq

由此得到结论:

(1)G₂F₁+G₂F₂=AD

(2)G₁G₂=AD

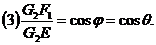
2、知识拓展

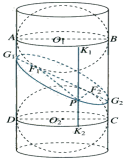
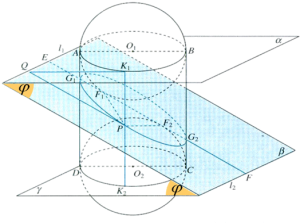
将图3-5中的两个圆拓广为球面，将矩形ABCD看成是圆柱面的轴截面，将EB、DF拓广为两个平面a、b，EF拓广为平面g，得到图3-6(课本第46页).21世纪教育网版权所有

你能猜想这个椭圆的两个焦点的位置吗？

猜想:两个焦点为两个球与斜截面的切点上，即过球心O₁、O₂分别作斜截面的垂线，其垂足F₁、F₂就可以能是焦点.21教育网

对截口上任一点P，证明PF₁+PF₂=定值

当点P与G₂重合时，有

G₂F₁＋G₂F₂＝AD

当点P不在端点时，连接PF₁，PF₂，则PF₁，PF₂分别是两个球面的切线，切点为F₁，F₂.

过P作母线，与两球面分别相交于K₁，K₂，则PK₁，PK₂分别是两球面的切线，切点为K₁，K₂

PF₁=PK₁，PF₂=PK₂，

PF₁+PF₂=PK₁+PK₂=AD

定理1 圆柱形物体的斜截口是椭圆.

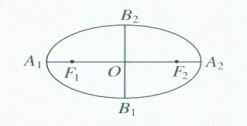
如上图，椭圆的焦点是F₁、F₂，B₁B₂是F₁F₂的中垂线.我们把A1A2叫做椭圆的长轴，B1B2叫做椭圆的短轴，F1F2叫做椭圆的焦距.如果长轴为2a，短轴为2b，那么焦距2c=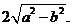21·cn·jy·com

3、椭圆的性质

思考：l₁，l₂与椭圆上的点有什么关系？

特殊点G₂

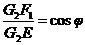=定值.

点P在椭圆的任意位置

PQ⊥l，PK₁⊥a

在Rt△PK₁Q，中∠QPK₁=j

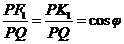=定值.

椭圆上任意一点到焦点F₁的距离与到直线l₁的距离之比为定值cosj.我们把直线l₁叫做椭圆的另一条准线.

同样，椭圆上任意一点到焦点F₂的距离与到直线l₂的距离之比为定值cosj.所以l₂是椭圆的另一条准线.2·1·c·n·j·y

记e=cosj，我们把e叫做椭圆的离心率.

请点击下载附件
			点击下载：平面与圆柱面的截线试题.zip

 

　　平面与圆柱面的截线考点！为大家介绍好了，如果大家还有什么问题的话，请直接拨打免费咨询电话：4000-121-121！有专业的老师为您解答！