弦切角的性质解题方法与技巧

　　弦切角的性质解题方法与技巧！弦切角的性质是中的学习重点，同学们学习这部分内容的时候，应该了解相关解题方法和技巧，提高学习效率。下面小编为大家分享弦切角的性质解题方法与技巧!希望对大家有所帮助！

 

 

弦切角的性质大汇总

 

　　弦切角的性质解题方法与技巧

 

（一）、弦切角的概念：

圆周角∠CAB，让射线AC绕点A旋转，产生无数个圆周角，当AC绕点A 旋转至与圆相切时，得∠BAE．提问：∠EAC有何特点？

弦切角的定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角.

【设计意图】观察由圆周角到弦切角的运动变化过程，发现弦切角与圆周角的区别与联系.注意引导孩子发现弦切角的三个要点，使孩子在形象、直观的学习活动中掌握新的概念.21cnjy.com

(二)观察、猜想

观察图形，提问:

(1)、图7(1)中，∠A与∠P有何关系？为什么？

(2)、图7(2)中，∠EAC与∠P有何共同点？

分析比较：既然图7(1)中∠A＝∠P，那么图7(2)中，∠EAC=∠P吗？

这一结论是否能成立呢？我们不妨从较特殊的情形考虑一下.

(1)、圆心O在弦切角∠BAC的边AC上， 此时显然有∠BAC=∠P=90°.

由此我们完全有信心提出一个猜想：弦切角等于它所夹的弧所对的圆周角.

(三)类比联想、论证

1、已经证明了较特殊的情形，下面考虑圆心在角内与角外两种情形.

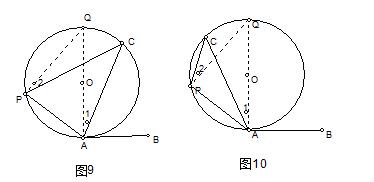
(2)、圆心在角外，作⊙O的直径AQ，连接PQ(如图9)，

则∠BAC=∠BAQ-∠1=∠APQ-∠2=∠APC.

(3)、圆心在角内，作⊙O的直径AQ，连接PQ(如图10)，

则∠BAC=∠BAQ+∠1=∠APQ+∠2=∠APC.

2、回顾证明的方法：将情形(2)、(3)都归至情形(1)，利用角的合成，对三种情形进行完全归纳，从而证明了上述的猜想，我们把所证得的结果取名为弦切角定理：弦切角等于它所夹的弧所对的圆周角.

 

请点击下载附件
			点击下载：弦切角的性质练题目.zip

 

　　弦切角的性质解题方法与技巧！为大家介绍好了，如果大家还有什么问题的话，请直接拨打免费咨询电话：4000-121-121！有专业的老师为您解答！