高考数学核心点及典型试题解析

　　高考临近，数学学科的复习也进入收官阶段。收官阶段的复习，理应有收官的意义，因此必须起到统领全局的作用。纵观高考数学诊断大纲以及历年高诊断题所体现的对考生能力的要求，我们不难看出，高考数学的较大核心点非它莫属——函数，及其辐射的诸多章节，包括与之相关的诸多数学思想。

　　函数是高考数学比例较大的章节，同时是高中数学体系的核心，无论是在高一时对必修1的学习还是在高三对函数模块的复习，均是旷日持久的。坦诚地讲，函数确是很多考生数学成绩不理想的起源或根源。所以，考生很有必要在考前将函数内容透彻理解、深刻领悟，以求不因此而在高考中留有遗憾。

　　函数所辐射的概念与性质众多，高度与角度难以把握。笔者认为，考生偏重知识点的堆积而未抓到贯穿其中的、事关本质理解的核心点，是未能将函数的学习明朗化的重要原因。站在系统化网络化的高度，找到函数概念与性质理解的共性(本质)，复习效率将大大提高，参见表1——

 

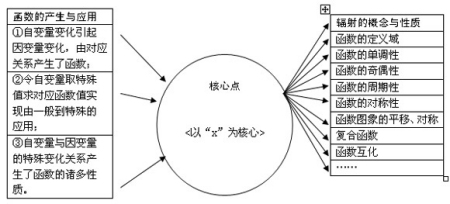
　　表1

　　现举高诊断题一例——

　　【2009全国卷高诊断题】函数f(x)定义域为R，若f(x+1)与f(x-1)都是奇函数，则(D)

　　A.f(x)是偶函数           B.f(x)是奇函数

　　C.f(x)=f(x+2)             D.f(x+3)是奇函数

　　【评析】在本题条件的应用上，很多考生得到了如下的错误结论：

　　根据f(x+1)为奇函数，得到f(x+1)=-f(-x-1)

　　根据f(x-1)为奇函数，得到f(x-1)=-f(-x+1)

　　这一现象是值得深思的，考生在已知f(x)为奇函数的条件下多数均能顺利得到f(x)=-f(-x)的结论，但当条件变为f(x+1)与f(x-1)时，便生搬硬套，导致失分，这正是对函数奇偶性理解不透所致。实际上，所谓函数的奇偶性，根据以“x”为核心，就是指当自变量“x”取原来的相反数“-x”时，f(x)与f(-x)之间的关系。因此，本题条件运用的结论应为：

　　根据f(x+1)为奇函数，得到f(x+1)=-f(-x+1)

　　根据f(x-1)为奇函数，得到f(x-1)=-f(-x-1)

　　智康教育：优秀的N对一个性化辅导、口碑好的家教品牌，提供小学数学、英语、语文、物理、化学等全科家教辅导，满足小学、小学、初中、中考、高中、高考等各类人群课外补习需求。