2008年高考数学复习：解析几何专题热点指导

　　天津市第四十二中学 张鼎言

　　3. 设A，B分别为椭圆-+-=1(a，b>0)的左、右顶点，椭圆长半轴的长等于焦距，且x=4为它的右准线。

　　(Ⅰ)、求椭圆的方程；

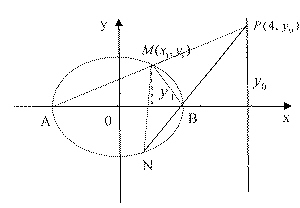
　　(Ⅱ)、设P为右准线上不同于点(4，0)的任意一点，若直线AP，BP分别与椭圆相交于异于A，B的点M、N，证明点B在以MN为直径的圆内。

　　解：(Ⅰ)由已知a=2c，-=4

　　故椭圆的方程为-+-=1

　　(Ⅱ)要证点B在以MN为直径的圆内，需证∠MBN>90°。用向量数量积方法要考虑B、M、N三个点的坐标，其中M、N两个点的坐标在运算上都有难度，我们转化为证明∠MBP<90°，这时用点P的坐标使问题简化。如图，不妨假定y0>0，y1>0

　　由平面几何，

　　-=-=-，

　　y0=-，

　　M在椭圆上，

　　即y12=-(12-3x12)

　　-=(x1-2，y1)，

　　-=(2，y0)

　　-·■=2(x1-2)+y0y1=2(x1-2)+-=2(x1-2)+-(2-x1)=-(2-x1)

　　而-2

　　∴-·■>0，

　　∴cos∠MBP>0，

　　∠MBP<90°，

　　∠MBN>90°