1.2.4有理数大小比较
学习目标:
1.掌握有理数大小的比较法则.
2.能利用数轴及绝对值的知识,比较两个有理数的大小.
重难点:
重点:掌握有理数大小的比较法则.
难点:比较有理数的大小
学法指导:
交流讨论,归纳类比
教学过程:
预习课本:
第12到第13页有理数大小比较
下面是我国5座城市某天的最低温度:
武汉-5 ℃,北京-10℃,上海0℃,哈尔滨-20℃ 广州10℃
(1)将这5座城市这一天的最低气温按照由低到高的顺序排列出来.
(2)这5座城市这一天的最低气温在温度计上对应的位置有什么规律?
(3)将这5座城市这一天的最低气温在数轴上表示出来,这些数的大小与它们在数轴上所表示的点的位置有什么关系?
归纳在数轴上表示的两个数,右边的数总比左边的数.
正数0,0负数,正数负数.
(4)比较下列两座城市之间最低气温的高低(填“高于”或“低于”)
北京__________武汉;北京__________哈尔滨.
(5)求出下列各数的绝对值:-5 -10 -20,并比较它们绝对值的大小.
(6)由上你发现了什么?
思考:结合绝对值,两个负数之间如何比较大小?
归纳两个负数,绝对值大的反而.
合作探究:
有理数大小的比较方法1:
借助数轴比较有理数的大小
(数轴比较法):
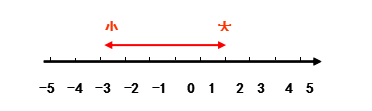
在数轴上表示的两个数,右边的数总比左边的数大.
有理数大小的比较方法2:
运用法则比较有理数的大小
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
结论:(1)正数大于0,负数小于0,正数大于负数;
自测提升:
例题探究:
例1:在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
例2:比较下列各数的大小.
(1)-(-3)和-(+2);
(2)-和-;
(3)|-|和-(-0.83)
例3:下列判断,正确的是( )
A.若a>b,则│a│>│b│ B.若│a│>│b│,则a>b
C.若ab>0,则│a│>│b│
巩固练习
1.在有理数0,│-(-3)│,-│+1000│,-(-5)中最大的数是( )
A.0 B.-(-5) C.-│+1000│ D.│-(-3)│
2.比较下列各对数的大小:
(1)-(-1)-(+2); (2) ;
(3); (4) -(-2).
3.将下列这些数用“<”连接.
