为什么这三点变化显著呢?下面结合实例详细为大家分析
(1)知识运用能力:压轴题
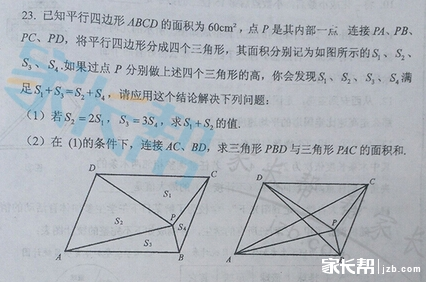
相信大家都知道,一份试卷的压轴题通常是试卷中最难的那个,但今年附中综测的压轴题,却为孩子们悄悄降低了难度,这本是一个考察大家经典“平行四边形一半模型综合运用”的问题(右图),早在十几年前的全国全国数学邀请测试当中出现过原图原题,但是本题作出了两处修改:
1)加入第1问,作为第2问的铺垫,第一问(左图)这个“一半模型”是解决第二问的关键所在,也是难度所在,在第一问攻克的前提下,孩子们是否可以利用第一问这个一半模型解决第二问,变成了第二问主要的考点!孩子们在知识运用能力在这个题目当中显露无疑!
2)条件的最后一行,加入了条件S1+S3=S2+S4,要知道这可是第一问最关键的条件,也是难度所在,孩子们是否可以利用这个结论解决第一问也就成了第一问主要的考点!同样非常考察孩子们知识运用能力!
(2)孩子的学习习惯:22题

这个题的问题:求出甲、乙共多少件?这个“共”成为了很多本会做这个题的孩子的易错点
18题:

这个题的难度在于:这题大家必然见过,高新一中2013年综测压轴题就曾对这个知识点进行过考察,孩子们不是第一次面对“在一个长方形中减去一个最大的正方形”这个经典操作了,但是是否可以真正领悟这个操作的本质就是“减去的正方形边长来自原长方形长宽中的较小边”,就决定了是否可以找到本题的四个答案!思维的缜密和严谨,可见一斑!
(3)逻辑思维的发散性:21题

这个题具有极强的操作性,虽然答案,但是“茶叶在箱中如何摆放”是一个很开放的问题,最值问题本就是数学中最考验发散性和创造力的问题,孩子们可以自由设计装箱方案,但是成功的方案离不开“尽量占满空间”的设想,实现这个设想并躲避“空间想象”带给我们的压力,“借助三视图”“长宽高之间的因倍关系”都是可以利用的技巧,这些知识需要孩子们在当初学习这些知识的时候对其有着一定的领悟!
16题:

这又是一个不容易处理的问题,本题可以说是逻辑的严谨和技巧的发散的一个结合,解决这个问题需要两个阶段:
1)圆心究竟走过的是什么样的轨迹?
解决这个问题,题中的条件“绕这3个圆滚动”非常重要,很多孩子审题不细,没有搞清运动方式,导致答非所问!“绕”很容易让我们联系到“圆弧”,准确的圆弧当然离不开准确的圆心和半径,不难发现这3个圆的圆心分别作为“绕”的圆心,这个轨迹是由三段圆弧构成!没有严谨,第一个过程无法高质量完成!
2)这个轨迹如何计算?
相信绝大多数孩子们都记得“弧长公式”,都记得求“弧长”的关键就是求半径和圆心角,半径本题并不难确定,圆心角需要孩子们发现中间那段圆弧的圆心、起点、终点构成了等边三角形,从而确定圆心角是60度!图形知识的穿插运用对孩子们的思维发散性考察尽在不言中!
7.未来的综测命题趋势如何?
答:(1)上述三种能力的考察势必更加助力!
(2)图形和应用题依然会是重点!
(3)试题更加生活,更加开放,更加灵活!
(4)试卷难度不会降低!
8.对于现在五年级的孩子,应该注意些什么才可以有效提高上述的三种能力呢?
答:一年又一年的经验表明两件事情非常、非常、非常重要
(1)课堂专注力 (2)课后巩固的及时有效
9.家长们可以注意些什么可以改善孩子的上述两个习惯?
答:(1)多与孩子学校里的班主任和任课老师沟通孩子在学校里的情况,发现问题并配合老师解决问题
(2)结合孩子所在小学在数学、语文方面的培养特点为孩子选择每一科选择一个课外补习班
(3)孩子课后的作业中出现的错题什么时候解决?如何解决?解决的如何?
(4)鼓励和批评结合,培养习惯-----多鼓励 纠正态度-----多批评
相关阅读推荐
