2017年北京十三中初一期中考试

点击领取>>>247套真题！2012-2018北京初一初二下学期期中诊断真题及答案

2017年北京十三中初一期中诊断！初一的时间要结束了，同学们要对自己的学习有所有交代，至少，不能在初一的时候有什么烂摊子还没收完，无论是这次的期中诊断也好，还是下一次的期末诊断也好，同学们加油！下面，小编为大家带来2017年北京十三中初一期中诊断。

2017年北京十三中初一期中诊断

点击了解>>>学而思爱智康初中期中3次进阶课&咨询课程请拨打：

2017年北京十三中初一期中诊断

培养数学思想，形成创造思维

假期延长，使得同学们有了更多的时间去挖深数学知识的内涵，捋清多个知识点之间的关系，培养自己在数学思想方面的素养。因篇幅所限，这里着重提到了分类思想、建模思想、转化思想、数形结合思想的培养办法。

（一）分类思想的培养

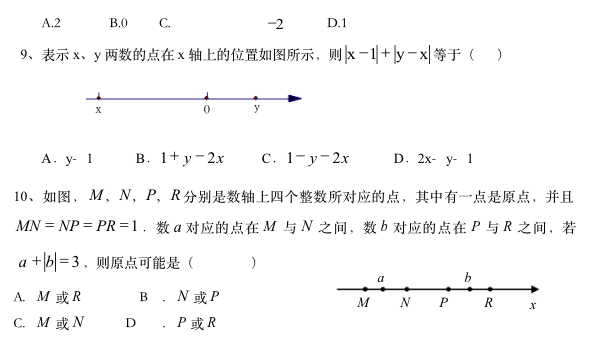
分类是根据数学本质属性的相同点和不同点，将数学研究对象分为不同种类的一种数学思想方法。如实数分为有理数和无理数，三角形分为锐角三角形、直角三角形、钝角三角形等。分类之所以会产生，是因为研究对象的不确定性。比如 x 的少有值为 2，我们知道 X 会有两种可能是 2 或 -2。其实是因为 x 是正数还是负数的不确定性导致的。再如等腰三角形两边为 3、5，求等腰三角形的周长，那么答案是分别为 11 或 13，这是由于 3、5 谁是腰谁是底边的不确定性导致的。

如果你认真观察，就会发现诊断时经常出错的是多个答案的问题。而出错的方向多数在于：想不到还有多个答案。那么我们就要注意很多问题在出现时的不确定性，看清是由于怎样的不确定，而导致了结果的不确定，就依照怎样的方向来分类解决问题。

（二）建模思想的培养

数学家笛卡尔曾说：" 一切问题都可以化归为数学问题，一切数学问题都可以化归为代数问题，一切代数问题都可以化归为方程问题。" 任何数学问题都是利用数学模型解决的，每一个数学概念和数学规则都是一个基本模型，模型化是一种重要的数学思想方法。

解决数学问题就是根据条件建立数学模型，再利用此模型建立数量关系求解。所以首先要熟练掌握各种基本的数学模型，然后才能在具体问题中识别和应用模型解题，那如何选择和构建数学模型呢？

1. 有则组之：如具备边角相等关系的可寻找全等模型，具备特殊角的可寻找三角模型。

2. 缺则补之：如图形已具备一边一角相等，可再添加一边或一角条件构造全等模型，已有特殊角但没有直角可作垂线构造直角三角形，已有共圆条件的可添加辅助圆。

3. 无则变之：如具备共点等线条件的，可把相关图形进行旋转；具备共线等角条件的，可把相关图形进行翻折；具备线段和差关系的，可把其中线段进行截长补短；具备线段比例关系的，可把有关图形进行缩放变换。注意，方程是解决数学问题的通用模型，也是基本思想，若问题中的数量不易直接，则应建立方程求解。

解题方法时的黄金法则：" 条件用足，模型完整 "。" 条件用足 " 指题中给出的所有相关条件得到充分利用，" 模型完整 " 指相关条件产生联系形成完整模型可以进行下一步和推理。" 模型完整 " 与 " 条件用足 " 是等价的，条件未用足说明模型不完整导致条件无法产生联系，模型不完整或找不到就是因为条件孤立分散无法利用。

（三）转化思想的培养

" 转化思想 " 就是把待解决或难解决的问题，通过某种转化手段，使他转化成已经解决或比较容易解决的问题，从而求得原问题的解答。这里问题在数学解题中几乎无处不在，在遇到一些数量关系复杂、隐蔽而难以解决的问题是，就可通过某种转化过程，使生疏的问题熟悉化、抽象的问题具体化、复杂的问题简单化，从而顺利解决问题。

获取完整版方法：

1.点击链接：https://jinshuju.net/f/qsfo1S 领取247套真题！2012-2018北京初一初二下学期期中诊断真题及答案，填写姓名、电话信息后即可跳转百度云盘地址，免费获取。

这一期的2017年北京十三中初一期中诊断小编就介绍到这里，诊断的意义没什么不同，都是为了检测你的学习状况的，所以，同学们一定要对你目前的学习有所重视才是。想了解相关课程的同学，请拨打学而思爱智康免费咨询电话：！

小编推荐：北京四中初一下期中语文答案

小编推荐：北京海淀区初一下期中历史试题及答案