三角形三边的关系知识要点

　　三角形三边的关系知识要点！我们发现，在初中数学诊断填空选择和解答题的压轴题中，常出现有关三角形知识点的题，同学们要努力掌握三角形的知识点哦，下面就是小编为大家整理的三角形三边的关系知识要点，供同学们参考使用。

 

三角形三边的关系知识要点

 

　　一般

　　设三角形三边为a,b,c则

　　a+b>c,a>c-b

　　b+c>a,b>a-c

　　a+c>b,c>b-a

　　如图，

 

 

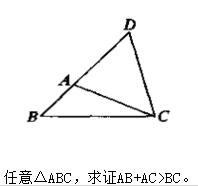
　　证明：在BA的延长线上取AD=AC

　　则∠D=∠ACD(等边对等角)

　　∵∠BCD>∠ACD

　　∴∠BCD>∠D

　　∴BD>BC(大角对大边)

　　∵BD=AB+AD=AB+AC

　　∴AB+AC>BC

　　三角形三边关系三角形的关系

　　编辑

　　一般三角形

　　

 

 

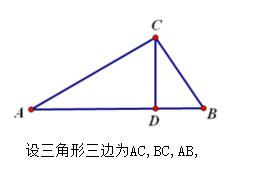
　　点D垂直于AB，为三角形ABC的高

　　如图，利用勾股定理，得

　　AC2-AD2=CD2① CB2-BD2=CD2 ②

　　①=②

　　AC2-AD2 =CB2-BD2

　　因为 AD+BD=AB

　　所以 AC2-(AB-BD)2=CB2-BD2 ③

　　同样也有AC2-AD2=CB2-(AB-AD)2 ④

　　③化简得：(AB2+CB2-AC2)÷2AB=BD

　　④化简得：(AB2-CB2+AC2)÷2AB=AD

 

　　三角形三边关系特殊

　　直角三角形

　　性质1：直角三角形两直角边的平方和等于斜边的平方。　 性质2：在直角三角形中，两个锐角互余。　 性质3：在直角三角形中，斜边上的中线等于斜边的一半。

　　性质4：直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。　性质5:如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：

　　(1) AD^2=BD·DC，

　　(2) AB^2=BD·BC ， 射影定理图

　　(3) AC^2=CD·BC 。 等积式 　(4)ABXAC=ADXBC (可用面积来证明) 　(5)直角三角形的外接圆的半径R=1/2BC,

　　(6)直角三角形的内切圆的半径r=1/2(AB+AC-BC)(公式一);r=AB*AC/(AB+BC+CA)(公式二)

　　

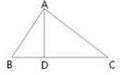
等腰直角三角形三边之比：1:1:根号二

 

　　小编推荐：

　　三角形的认识讲解

　　三角形全等的判定讲解

　　三角形三边的关系解题

 

　　以上就是小编特意为大家整理的三角形三边的关系知识要点，同学们如果在学习中有什么疑问，欢迎拨打爱智康免费电话：!那里有专业的老师为大家解答。