三角形的重心知识要点

　　三角形的重心知识要点！三角形重心是三角形三条中线的交点。当几何体为匀质物体时，重心与形心重合。三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心) 。下面就是小编为大家整理的三角形的重心知识要点，供同学们参考使用。希望可以帮助到大家。

 

 

三角形的重心知识要点

 

 

 

　　初中关于三角形重心的几何问题

　　提示：我们知道三角形三条中线的交点叫做三角形重心，重心到顶点的距离与重心到该顶点对边中点的距离之比为2：1请用次性质解决下列问题

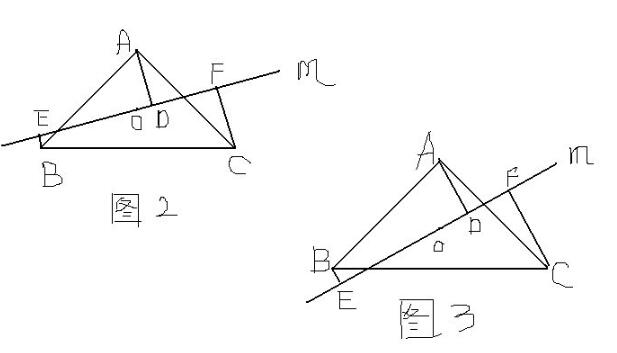
　　1如图，点O为等腰直角三角形的重心，角CAB=90，直线m过O,过ABC分别作直线m的垂线，垂足分别为点DEF

　　当直线m绕点A旋转到与BC不平行时，分别探究以下两种情况下，线段AD,BE,CF,之间有什么关系，并证明。

 

　　AD+BE=CF

　　证明：

　　连接CO并延长交AB于M，作MN⊥直线m，垂足为N

　　因为O是等边三角形ABC的内心

　　所以CM是∠ACB的平分线

　　根据“三线合一”性质知M是AB的中点

　　因为AD⊥直线m，BE⊥直线m，MN⊥直线m

　　所以AD//MN//BE

　　所以MN是梯形ABED的中位线

　　所以2MN=AD+BE

　　因为CF⊥直线m

　　所以CF//MN

　　所以△COF∽△MON

　　因为等边三角形的内心与重心重合

　　所以O是三角形ABC的重心

　　所以CO=2OM

　　所以CF=2MN

　　所以AD+BE=CF

 

　　小编推荐：

　　三角形的重心讲解

　　三角形的外角讲解

　　三角形的外角方法

 

　　以上就是小编特意为大家整理的三角形的重心知识要点，同学们如果在学习中有什么疑问，欢迎拨打爱智康免费电话：!那里有专业的老师为大家解答。